My recent work in condensed matter is focused on magnetic impurities in superconductors of mixed order parameter symmetry. The most interesting behavior occurs in the case when the s-wave component of the order parameter is subdominant, as may occur e.g. in some high-temperature superconductors. At very low temperature the density of states near the Fermi level undergoes a discontinuous transition as a function of some parameter other than temperature. This has a strong effect on all low energy properties.

I also study the nonlinear dynamics of neurons and neural systems. These are strongly nonlinear systems with rich internal dynamics, chaos, multimodal response, resonance and the ability to perform nontrivial transformations of incoming signals. Even seemingly simple models lead to surprising outcomes. One of such surprises is a multimodal transition involving the change of parity of response modes in a periodically stimulated resonant neuron. I discovered the transition, Physical Review 80, 051914 (2009), and analyzed it in a subsequent series of papers. I also showed by comparing results of theoretical calculations to experimental data of a Japanese group N. Takahashi, Y. Hanyu, T. Musha, R. Kubo, and G. Matsumoto, Physica D 43, 318 (1990), that their data provides an experimental proof for the existence of the odd-all multimodal transition, see below.

 

 

There is also an even-all transition in the Hodgkin-Huxley model in the vicinity of the main resonance (see the Bistability and resonance... paper below). These effects exist also in other nonlinear systems.

Selected recent publications
 

L. S. Borkowski

Magnetic impurity-induced states in the gap of an s± superconductor  

Phys. Stat. Sol. B 250, 615 (2013)

DOI: 10.1002/pssb.201200750

Abstract

 

L. S. Borkowski

Multimodal transition and excitability of a neural oscillator

Acta Phys. Pol. A 122, 776 (2012)

Abstract

 

L. S. Borkowski

Response of the Hodgkin-Huxley neuron to a periodic sequence of biphasic pulses

Acta Phys. Pol. A 125, 145 (2014)

Abstract

 

L. S. Borkowski

Bistability and resonance in the periodically stimulated Hodgkin-Huxley model with noise

Phys. Rev. E 83, 051901 (2011)

URL:

http://link.aps.org/doi/10.1103/PhysRevE.83.051901

DOI: 10.1103/PhysRevE.83.051901

Abstract

L. S. Borkowski
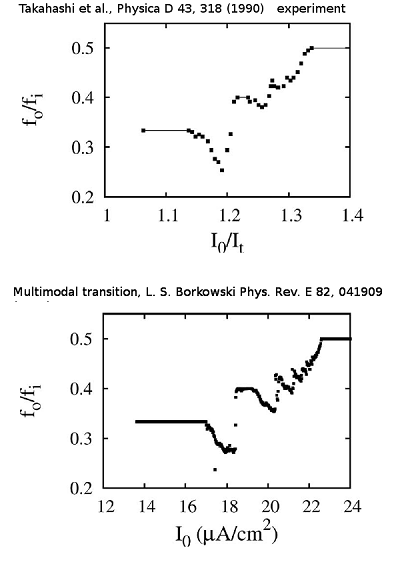
Multimodal transition and stochastic antiresonance in squid giant axons
Phys. Rev. E 82, 041909 (2010)

URL:

http://link.aps.org/doi/10.1103/PhysRevE.82.041909

DOI:

10.1103/PhysRevE.82.041909

Abstract

L. S. Borkowski
Magnetic impurity transition in a (d+s)-wave superconductor
Phys. Status Solidi B 247, 602–604 (2010)

DOI: 10.1002/pssb.200983023

Abstract
 

L. S. Borkowski

Nonlinear dynamics of Hodgkin-Huxley neurons

Wydawnictwo Naukowe UAM, Poznan (2010) (Adam Mickiewicz University Press)

ISBN 978-83-232-2106-7

78 pages, 71 figures

This monograph describes the dynamics of the Hodgkin-Huxley neurons stimulated by periodic and stochastic stimuli. In the high frequency regime there is a multimodal transition between the odd-only modes and the state with both odd and even modes. This singularity appears in the presence of noise as a stochastic anti-resonance. The competition of different parity modes is reflected also in the structure of the resonances, where even and odd phase-locked states are separated by crossover regimes. The boundaries between various mode-locked states form complicated patterns. The relation between the output frequency and stimulus amplitude near the excitation threshold is often continuous even in the absence of noise. Models of regular spiking excitatory and inhibitory cells of mammalian cortex are also studied within this framework. The obtained high variability of response agrees with experiments in vivo.

 

 

The following picture is a color version of Fig. 3.9 from the monograph.

The blue color refers to k=5:2, yellow refers to k=3, red refers to k=4.

 

 

L. S. Borkowski

Resonant response of a Hodgkin-Huxley neuron to a spike train input

BMC Neuroscience 2009, 10(Suppl 1):P250

DOI:10.1186/1471-2202-10-S1-P250

 

L. S. Borkowski
Response of a Hodgkin-Huxley neuron to a high-frequency input
Phys. Rev. E 80, 051914 (2009)

URL:

http://link.aps.org/doi/10.1103/PhysRevE.80.051914

DOI:

10.1103/PhysRevE.80.051914

Abstract

L. S. Borkowski
Zero temperature phase diagram of a d-wave superconductor with Anderson impurities
Acta Phys. Pol. A 115, 120-122 (2009)

L. S. Borkowski
Density of states of s+d-wave superconductor with Anderson impurities
Journal of Physics: Conference Series 150 (2009) 052023

DOI: 10.1088/1742-6596/150/5/052023

L. S. Borkowski and Z. Jacyna-Onyszkiewicz
Spatial distribution of Gaussian fluctuations of the molecular field and magnetization in the pyramid-like Ising nanoscopic system interacting with the substrate

Surf. Sci. 603, 27-32 (2009)

DOI:10.1016/j.susc.2008.10.028

Abstract

 

L. S. Borkowski
Phase diagram of a d-wave superconductor with Anderson impurities
Phys. Rev. B 78, 020507(R) (2008)

URL:

http://link.aps.org/doi/10.1103/PhysRevB.78.020507

DOI:

10.1103/PhysRevB.78.020507

Abstract

L. S. Borkowski and Z. Jacyna-Onyszkiewicz
Spatial distribution of magnetization in the pyramid-like Ising nanoscopic system interacting with the substrate
Acta Phys. Pol. A 112, 1223-1230 (2007)